being the
Revised Report on the Algorithmic Language ALGOL 60
(dedicated to the memory of William Turanski)
by J. W. Backus, F. L. Bauer, J. Green, C. Katz, J. McCarthy,
P. Naur, A. J. Perlis, H. Rutishauser, K. Samelson, B. Vauquois,
J. H. Wegstein, A. van Wijngaarden and M. Woodger
as modified by
R. M. De Morgan, I. D. Hill and B. A. Wichmann
under the authority of IFIP Working Group 2.1.
|
If any man, who shall desire a more particular account of the several Alterations . . . . shall take the pains to compare the present Book with the former; we doubt not but the reason of the change may easily appear. |
|
| Preface to Book of Common Prayer 1662. |
For the history of ALGOL 60 up to April 1962, the Revised Report on ALGOL 60 (Naur, 1963) should be consulted.
Following the publication of the Revised Report, responsibility for ALGOL was transferred to Working Group 2.1 of IFIP Technical Committee 2. In 1964 WG2.1 produced reports on a subset of the language (IFIP, 1964a), and on input/output procedures (IFIP, 1964b), but thereafter devoted most of its attention to a proposed new language that was eventually adopted as ALGOL 68 – a separate development, with which the present Report is not concerned.
Additional proposals for a different subset and for input/output were proposed by the European Computer Manufacturers' Association (ECMA) (1965) and by the Association for Computing Machinery (ACM) (Knuth et al, 1964) respectively.
In 1972 a version of the Revised Report, together with the various proposals on subsets and input/output, was published by the International Organization for Standardization as ISO Recommendation 1538 (1972), but IFIP refused to recognise this document as valid. Three subsets were given as Level 1 (ECMA, with recursion), Level 2 (ECMA) and Level 3 (IFIP), the full language being called Level 0.
Meanwhile, various defects have been noted in the language definition which have unnecessarily hindered the use of ALGOL. Although the existence of subsets has given some assistance to the compiler-writer and user of the language, numerous problems exist, some of which were noted in the Revised Report.
Hence the need for a detailed commentary and standard interpretation has become apparent. Such a commentary is now available, defining the modifications necessary to produce this Report from the Revised Report. A preliminary version was discussed at the 1974 meeting of Working Group 2.1 at Breukelen. A revised version appeared in ALGOL Bulletin No. 38, together with a questionnaire and a request for comments. A further revision was based on the replies, and discussed at the 1975 meeting of Working Group 2.1 at Munich, where it was recommended for publication as an IFIP document.
The algorithmic language has two different kinds of representation – reference and hardware – and the development described in the sequel is in terms of the reference representation. This means that all objects defined within the language are represented by a given set of symbols – and it is only in the choice of symbols that other representations may differ. Structure and content must be the same for all representations.
Each one of these:
The purpose of the algorithmic language is to describe computational processes. The basic concept used for the description of calculating rules is the well-known arithmetic expression containing as constituents numbers, variables, and functions. From such expressions are compounded, by applying rules of arithmetic composition, self-contained units of the language – explicit formulae – called assignment statements.
To show the flow of computational processes, certain nonarithmetic statements and statement clauses are added which may describe, e.g. alternatives, or iterative repetitions of computing statements. Since it is sometimes necessary for the function of the statements that one statement refers to another, statements may be provided with labels. A sequence of statements may be enclosed between the statement brackets begin and end to form a compound statement.
Statements are supported by declarations which are not themselves computing instructions, but inform the translator of the existence and certain properties of objects appearing in statements, such as the class of numbers taken on as values by a variable, the dimension of an array of numbers, or even the set of rules defining a function. A sequence of declarations followed by a sequence of statements and enclosed between begin and end constitutes a block. Every declaration appears in a block in this way and is valid only for that block.
A program is a block or a compound statement that is contained only within a fictitious block (always assumed to be present and called the environmental block), and that makes no use of statements or declarations not contained within itself, except that it may use such procedure identifiers and function designators as may be assumed to be declared in the environmental block.
The environmental block contains procedure declarations for standard functions, input and output operations, and possibly other operations to be made available without declaration within the program. It also contains the fictitious declaration, and initialisation, of own variables (see Section 5).
In the sequel the syntax and semantics of the language will be given.
Whenever the precision of arithmetic is stated as being in general not specified, or the outcome of a certain process is left undefined or said to be undefined, this is to be interpreted in the sense that a program only fully defines a computational process if the accompanying information specifies the precision assumed, the kind of arithmetic assumed, and the course of action to be taken in all such cases as may occur during the execution of the computation.
The syntax will be described with the aid of metalinguistic formulae (Backus, 1959). Their interpretation is best explained by an example:
<ab> ::= ( | [ | <ab> ( | <ab> <d>
Sequences of characters enclosed in the bracket <> represent metalinguistic variables whose values are sequences of symbols. The marks ::= and | (the latter with the meaning of 'or') are metalinguistic connectives. Any mark in a formula, which is not a variable or a connective, denotes itself (or the class of marks which are similar to it). Juxtaposition of marks and/or variables in a formula signifies juxtaposition of the sequences denoted. Thus the formula above gives a recursive rule for the formation of values of the variable <ab>. It indicates that <ab> may have the value ( or [ or that given some legitimate value of <ab>, another may be formed by following it with the character ( or by following it with some value of the variable <d>. If the values of <d> are the decimal digits, some values of <ab> are:
[(((1(37( (12345( ((( [86
In order to facilitate the study, the symbols used for distinguishing the metalinguistic variables (i.e. the sequence of characters appearing within the brackets <> as ab in the above example) have been chosen to be words describing approximately the nature of the corresponding variable. Where words which have appeared in this manner are used elsewhere in the text they will refer to the corresponding syntactic definition. In addition some formulae have been given in more than one place.
Definition:
<empty> ::=
(i.e. the null string of symbols).
The reference language is built up from the following basic symbols:
<basic symbol> ::= <letter> | <digit> | <logical value> | <delimiter>
<letter> ::= a | b | c | d | e | f | g | h | i | j | k | l |
m | n | o | p | q | r | s | t | u | v | w | x | y | z | A |
B | C | D | E | F | G | H | I | J | K | L | M | N | O | P |
Q | R | S | T | U | V | W | X | Y | Z
This alphabet may be arbitrarily restricted, or extended with any other distinctive character (i.e. character not coinciding with any digit, logical value or delimiter).
Letters do not have individual meaning. They are used for forming
identifiers and strings. They are used for forming identifiers and strings (see
Sections 2.4 Identifiers, 2.6 Strings). Within this report the letters (from an extended alphabet) 
,
, 
and 
are sometimes used and are understood as not being available to the programmer. If an
extended alphabet is in use, that does include any of these letters, then their uses within this report
must be systematically changed to other letters that the extended alphabet does not include.
<digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
Digits are used for forming numbers, identifiers, and strings.
<logical value> ::= true | false
The logical values have a fixed obvious meaning.
<delimiter> ::= <operator> | <separator> | <bracket> | <declarator> | <specificator>
<operator> ::= <arithmetic operator> | <relational operator> | <logical operator> |
<sequential operator>
<arithmetic operator> ::= + | - | 
| / | ÷ | 
<relational operator> ::= < | 
| = | 
| > | 
<logical operator> ::= 
| 
| 
| 
| ¬
<sequential operator> ::= go to | if | then | else | for | do
<separator> ::= , | . | 10 | : | ; | := | 
| step | until | while | comment
<bracket> ::= ( | ) | [ | ] | ` | ' | begin | end
<declarator> ::= own | Boolean | integer | real | array | switch | procedure
<specificator> ::= string | label | value
Delimiters have a fixed meaning which for the most part is obvious or else will be given at the appropriate place in the sequel.
Typographical features such as blank space or change to a new line have no significance in the reference language. They, however, be used freely for facilitating reading.
For the purpose of including text among the symbols of a program the following "comment" conventions hold:
The sequence of basic symbols:
; comment <any sequence of zero or more
characters not containing ;>;
begin comment <any sequence of zero or more
characters not containing ;>;
end <any sequence of zero or more
characters not containing end or ; or else>
|
is equivalent to
; begin end |
By equivalence is here meant that any of the three structures shown in the left hand column may be replaced, in any occurrence outside of strings, by the symbol shown on the same line in the right hand column without any effect on the action of the program. It is further understood that the comment structure encountered first in the text when reading from left to right has precedence in being replaced over later structures contained in the sequence.
<identifier> ::= letter> | <identifier> <letter> | <identifier> <digit>
q Soup V17a a34kTMNs MARILYN
2.4.3. Semantics
Identifiers have no inherent meaning, but serve for
the identification of simple variables, arrays, labels, switches, and
procedures. They may be chosen freely. Identifiers also act as formal parameters
of procedures, in which capacity they may represent any of the above entities, or a string.
The same identifier cannot be used to denote two different quantities except when these quantities have disjoint scopes as defined by the declarations of the program (see Section 2.7 Quantities, kinds and scopes and Section 5 Declarations). This rule applies also to the formal parameters of procedures, whether representing a quantity or a string.
<unsigned integer> ::= <digit> | <unsigned integer> <digit>
<integer> ::= <unsigned integer> | + <unsigned integer> | - <unsigned integer>
<decimal fraction> ::= . <unsigned integer>
<exponential part> ::= 10 <integer>
<decimal number> ::= <unsigned integer> | <decimal fraction> |
<unsigned integer> <decimal fraction>
<unsigned number> ::= <decimal number> | <exponential part> |
<decimal number> <exponential part>
<number> ::= <unsigned number> | + <unsigned number> | - <unsigned number>
0 -200.084 -.08310-02 177 + 07.43108 -107 .5384 9.3410+10 10-4 +0.7300 210-4 +10+5
2.5.3. Semantics
Decimal numbers have their conventional meaning.
The exponent part is scale factor expressed as an integral power of 10.
2.5.4. Types
Integers are of the type integer. All other
numbers are of type real (see Section 5.1 Type declarations).
<proper string> ::= <any sequence of characters not containing ` or ' > | <empty> <open string> ::= <proper string> | <proper string> <closed string> <open string> <closed string> ::= `<open string>' <string> ::= <closed string> | <closed string> <string>
`5k,,-`[[[`
2.6.3. Semantics
In order to enable the language to handle sequences of characters the string quotes ` and ' are introduced.
The characters available within a string are a question of hardware representation, and further
rules are not given in the reference language. However, it is recommended that visible characters,
other than and ", should represent themselves, while invisible characters other than space should
not occur within a string. To conform with Draft ISO/TR 1672, a space may stand for itself, although
in this document the character is used to represent a space.
To allow invisible, or other exceptional characters to be used, they are represented within either matching string quotes or a matched pair of the " symbol. The rules within such an inner string are unspecified, so if such an escape mechanism is used a comment is necessary to explain the meaning of the escape sequence.
A string of the form <closed string><string> behaves as if it were the string formed by deleting the closing string quote of the closed string and the opening string quote of the following string (together with any layout characters between them).
Strings are used as actual parameters of procedures (see Sections 3.2 Function designators and 4.7 Procedure statements).
The following kinds of quantities are distinguished: simple variables, arrays, labels, switches, and procedures.
The scope of a quantity is the set of statements and expressions in which the declaration of the identifier associated with that quantity is valid. For labels see Section 4.1.3.
A value is an ordered set of numbers (special case: a single number), an ordered set of logical values (special case: a single logical value), or a label.
Certain of the syntactic units are said to possess values. These values will in general change during the execution of the program. The values of expressions and their constituents are defined in Section 3. The value of an array identifier is the ordered set of values of the corresponding array of subscripted variables (see Section 3.1.4.1).
The various types (integer, real, Boolean) basically denote properties of values. The types associated with syntactic units refer to the values of these units.
In the language the primary constituents of the programs describing algorithmic processes are arithmetic, Boolean, and designational expressions. Constituents of these expressions, except for certain delimiters, are logical values, numbers, variables, function designators, labels, switch designators, and elementary arithmetic, relational, logical, and sequential operators. Since the syntactic definition of both variables and function designators contains expressions, the definition of expressions, and their constituents, is necessarily recursive.
<expression> ::= <arithmetic expression> |
<Boolean expression> | <designational expression>
<variable identifier> ::= <identifier>
<simple variable> ::= <variable identifier>
<subscript expression> ::= <arithmetic expression>
<subscript list> ::= <subscript expression> |
<subscript list> , <subscript expression>
<array identifier> ::= <identifier>
<subscripted value> ::= <array identifier>[<subscripted list>]
<variable> ::= <simple variable> | <subscripted variable>
epsilon detA a17 Q[7, 2] x[sin(n
3.1.3. Semantics
A variable is a designation given to a single value. This value may be used in expressions for
forming other values and may be changed at will by means of assignment statements (see Section
4.2). The type of the value of a particular variable is defined in the declaration for the variable itself
(see Section 5.1 Type declarations) or for the corresponding array identifier (see Section 5.2 Array declarations).
3.1.4. Subscripts
3.1.4.1. Subscripted variable designate values which are components of multidimensional arrays
(see Section 5.2 Array declarations). Each arithmetic expression of the subscript list occupies one
subscript position of the subscripted variable and is called a subscript. The complete list of subscripts
is enclosed in the subscript brackets [ ]. The array component referred to by a subscripted
variable is specified by the actual numerical value of its subscripts (see Section 3.3 Arithmetic expressions).
3.1.4.2. Each subscript position acts like a variable of integer type and the evaluation of the subscript is understood to be equivalent to an assignment to this fictitious variable (see Section 4.2.4). The value of the subscripted variable is defined only if the value of the subscript expression is within the subscript bounds of the array (see Section 5.2 Array declarations).
3.1.5. Initial values of variables
The value of a variable, not declared own, is undefined from entry into the block in which it is declared
until an assignment is made to it. The value of a variable declared own is zero (if arithmetic)
or false (if Boolean) on first entry to the block in which it is declared and at subsequent entries it
has the same value as at the preceding exit from the block.
<procedure identifier> ::= <identifier>
<actual parameter> ::= <string> | <expression> |
<array identifier> | <switch identifier> | <procedure identifier>
<letter string> ::= <letter> | <letter string> <letter>
<parameter delimiter> ::= , | ) <letter string> : (
<actual parameter list> ::= <actual parameter> |
<actual parameter list> <parameter delimiter> <actual parameter>
<actual parameter part> ::= <empty> | ( <actual parameter list> )
<function designator> ::= <procedure identifier> <actual parameter part>
sin(a - b) J(v + s, n) R S(s - 5) Temperature:(T) Pressure:(P) Compile(`:=') Stack:(Q)
3.2.3. Semantics
Function designators define single numerical or logical values which result through the application
of given sets of rules defined by a procedure declaration (see Section 5.4 Procedure declarations) to
fixed sets of actual parameters. The rules governing specification of actual parameters are given in
Section 4.7 Procedure statements. Not every procedure declaration defines rules for determining the
value of a function designator.
3.2.4. Standard functions
Certain standard functions and procedures are declared in the environmental block with the following procedure identifiers:
abs, iabs, sign, entier, sqrt, sin, cos, arctan, ln, exp, inchar, outchar, length, outstring, outterminator, stop, fault, ininteger, outinteger, inreal, outreal, maxreal, minreal, maxint and epsilon.
For details of these functions and procedures, see the specification of the environmental block given as Appendix 2.
<adding operator> ::= + | - <multiplying operator> ::=
Primaries:
7.39410-8 sum w[i + 2, 8] cos(y + z
Factors:
omega sum
Terms:
U omegaSimple arithmetic expressions:
U - Yu + omega
Arithmetic expressions:
w
3.3.3. Semantics
An arithmetic expression is a rule for computing a numerical value. In the case of simple arithmetic
expressions this value is obtained by executing the indicated arithmetic operations on the actual
numerical values of the primaries of the expression, as explained in detail in Section 3.3.4 below.
The actual numerical value of a primary is obvious in the case of numbers. For variables it is the
current value (assigned last in the dynamic sense), and for function designators it is the value arising
from the computing rules defining the procedure (see Section 5.4.4 Values of function designators)
when applied to the current values of the procedure parameters given in the expression. Fi-nally,
for arithmetic expression enclosed in parenthesis the value must through a recursive analysis
be expressed in terms of the values of primaries of the other three kinds.
In the more general arithmetic expressions, which include if clauses, one out of several simple arithmetic expressions is selected on the basis of the actual values of the Boolean expressions (see Section 3.4 Boolean expressions). This selection is made as follows: The Boolean expressions of the if clauses are evaluated one by one in sequence from left to right until one having the value true is found. The value of the arithmetic expression is then the value if the first arithmetic expression following this Boolean (the longest arithmetic expression found in this position is understood). If none of the Boolean expressions has the value true, then the value of the arithmetic expression is the value of expression following the final else.
The order of evaluation of primaries within an expression is not defined. If different orders of evaluation would produce different results, due to the action of side effects of function designators, then the program is undefined.
In evaluating an arithmetic expression, it is understood that all the primaries within that expression are evaluated, except those within any arithmetic expression that is governed by an if clause but not selected by it. In the special case where an exit is made from a function designator by means of a go to statement (see Section 5.4.4), the evaluation if the expression is abandoned, when the go to statement is executed.
3.3.4. Operators and types
Apart from the Boolean expressions of clauses, the constituents of simple arithmetic expressions
must be of real or integer types (see Section 5.1 Type declaration). The meaning of the basic operators
and the types of the expressions to which they lead are given by the following rules:
3.3.4.1. The operators +, -, and have the conventional meaning
(addition, subtraction, and multiplication). The type of the expression
will by integer if both of the operands are of integer
type, otherwise real.
3.3.4.2. The operations <term> / <factor> and <term> ÷ <factor> both denote division. The operations are undefined if the factor has the value zero, but are otherwise to be understood as a multiplication of the term by the reciprocal of the factor with due regard to the rules of precedence (see Section 3.3.5). Thus for example
a/b
means
((((a
The operator / is defined for all four combinations of real and integer types and will yield results of real type in any case. The operator ÷ is defined only for two operands both of integer type and will yield a result of integer type. If a and b are of integer type, then the value of a ÷ b is given by the function:
integer procedure div(a, b); value a, b;
integer a, b;
if b = 0 then
fault( `divbyzero' , a)
else
begin integer q, r;
q := 0; r := iabs(a);
for r := r - iabs(b) while r 0 do q := q + 1;
div := if a < 0 b > 0 then -q else q
end div;
3.3.4.3. The operation <factor> <factor>
denotes exponentiation, where the factor is the base and the primary is
the exponent. Thus for example
2while
2
If r is of real type and x of either real or integer type, then the value of xr is given by the function:
real procedure expr(x, r); value x, r;
real x, r;
if x > 0.0 then
expr := exp(r ln(x))
else if x = 0.0 r > 0.0 then
expr := 0.0
else
fault( `exprundefined' , x)
If i and j are both of integer type, then the value of ij is given by the function:
integer procedure expi(i, j); value i, j; integer i, j; if j < 0
If n is of integer type and x of real type, then the value of xn is given by the function:
real procedure expn(x, n); value x, n; real x; integer n; if n = 0
The call of the procedure fault denotes that the action of the program is undefined. It is understood that the finite deviations (see Section 3.3.6) of using the exponentiation operator may be different from those of using the procedures expr and expn.
3.3.4.4. Type of a conditional expression
The type of an arithmetic expression of the form
if B then SAE else AE
does not depend upon the value of B. The expression is of real type if either SAE or AE is real and is of integer type otherwise.
3.3.5. Precedence of operators
The sequence of operations within one
expression is generally from left to right, with the following
additional rules:
3.3.5.1. According to the syntax given in Section 3.3.1 the following rules of precedence hold:
first:
3.3.5.2. The expression between a left parenthesis and the matching right parenthesis is evaluated by itself and this value is used in subsequent calculations. Consequently the desired order of execution of operations within an expression can always be arranged by appropriate positioning of parentheses.
3.3.6. Arithmetics of real quantities.
Numbers and variables of real type must be interpreted in the sense of numerical analysis, i.e. as
entities defined inherently with only a finite accuracy. Similarly, the possibility of the occurrence of
a finite deviation from the mathematically defined result in any arithmetic expression is explicitly
understood. No exact arithmetic will be specified, however, and it is indeed understood that different
implementations may evaluate arithmetic expressions differently. The control of the possible
consequences of such differences must be carried out by the methods of numerical analysis. This
control must be considered a part of the process to be described, and will therefore be expressed in
terms of the language itself.
<relational operator> ::= < |
x = -2 Y > V
3.4.3. Semantics
A Boolean expression is a rule for computing a
logical value. The principles of evaluation are entirely analogous to
those given for arithmetic expressions in Section 3.3.3.
3.4.4. Types
Variables and function designators entered as Boolean
primaries must be declared Boolean (see Section 5.1. Type
declarations and Section 5.4.4. Value of function designators).
3.4.5. The operators
The relational operators <, , =, , > and have their conventional meaning (less than, less than
or equal to, equal to, greater than or equal to, greater than, not equal to). Relations take on the value
true whenever the corresponding relation is satisfied for the expressions involved, otherwise false.
The meaning of the logical operators ¬ (not), (and),
(or), (implies), and (equivalent), is given
by the following function table.
b1 |
false |
false |
true |
true |
¬b1 |
true |
true |
false |
false |
3.4.6. Precedence of operators
The sequence of operations within one
expression is generally from left to right, with the following
additional rules:
3.4.6.1. According to the syntax given in Section 3.4.1 the following rules of precedence hold:
3.4.6.2. The use of parentheses will be interpreted in the sense given in Section 3.3.5.2.
<label> ::= <identifier> | <unsigned integer>
<switch identifier> ::= <identifier>
<switch designator> ::= <switch identifier>[<subscript expression>]
<simple designational expression> ::= <label> |
<switch designator> | (<designational expression>)
<designational expression> ::= <simple designational expression> |
<if clause> <simple designational expression>
else <designational expression>
17 p9 Choose[n - 1] Town [if y < 0 then N else N + 1] if Ab < c then 17 else q[if w
3.5.3. Semantics
A designational expression is a rule for obtaining a label of a statement (see Section 4 Statements).
Again the principle of the evaluation is entirely analogous to that of arithmetic expressions (see
Section 3.3.3). In the general case the Boolean expressions of the if clauses will select a simple
designational expression. If this a label the desired result is already found. A switch designator refers
to the corresponding switch declaration (see Section 5.3 Switch declarations) and by the actual
numerical value of its subscript expression selects one of the designational expressions listed in the
switch declaration by counting these from left to right. Since the designational expression thus selected
may again be a switch designator this evaluation is obviously a recursive process.
3.5.4. The subscript expression
The evaluation of the subscript
expression is analogous to that of subscripted variables (see Section
3.1.4.2). The value of a switch designator is defined only if the
subscript expression assumes one of the positive values 1, 2, 3, ..., n,
where n is the number of entries in the switch list.
The units of operation within the language are called statements. They will normally be executed consecutively as written. However, this sequence of operations may be broken by go to statements, which define their successor explicitly, shortened by conditional statements, which may cause certain statements to be skipped, and lengthened by for statements which cause certain statements to be repeated.
In order to make it possible to define a specific dynamic succession, statements may be provided with labels.
Since sequences of statements may be grouped together into compound statements and blocks the definition of statement must necessarily be recursive. Also since declarations, described in Section 5, enter fundamentally into the syntactic structure, the syntactic definition of statements must suppose declarations to be already defined.
<unlabelled basic statement> ::= <assignment statement> |
<go to statement> | <dummy statement> | <procedure statement>
<basic statement> ::= <unlabelled basic statement> |
<label>: <basic statement>
<unconditional statement> ::= <basic statement> |
<compound statement> | <block>
<statement> ::= <unconditional statement> |
<conditional statement> | <for statement>
<compound tail> ::= <statement> end |
<statement> ; <compound tail>
<block head> ::= begin <declaration> |
<block head> ; <declaration>
<unlabelled compound> ::= begin <compound tail>
<unlabelled block> ::= <block head> ; <compound tail>
<compound statement> ::= <unlabelled compound> |
<label>: <compound statement>
<block> ::= <unlabelled block> | <label>: <block>
<program> ::= <block> | <compound statement>
This syntax may be illustrated as follows: Denoting arbitrary statements, declarations, and labels, by the letters S, D, L, respectively, the basic syntactic units take the forms:
Compound statement:
L:L: ... begin S; S; ... S; S endBlock:
L:L: ... begin D; D; .. D; S; S; ... S; S end
It should be kept in mind that each of the statements S may again be a complete compound statement or a block.
Basic statements:
a := p + q go to Naples START:CONTINUE: W := 7.993
Compound statements:
begin x := 0; for y := 1 step 1 until n do x := x + A[y];
if x > q then go to STOP
else if x > w-2 then go to S;
Aw: St: W := x + bob
end
Block:
Q: begin integer i, k; real w;
for i:=1 step 1 until m do
for k := i + 1 step 1 until m do
begin w := A[i, k];
A[i, k] := A[k, i];
A[k, i] := w
end for i and k
end block Q
4.1.3. Semantics
Every block automatically introduces a new level of nomenclature. This is realised as follows: Any
identifier occurring within the block may through a suitable declaration (see Section 5 Declarations)
be specified to be local to the block in question. This means (a) that the entity specified by
this identifier inside the block has no existence outside it and (b) that any entity represented by this
identifier outside the block is completely inaccessible inside the block.
Identifiers (except those representing labels) occurring within a block and not being declared to this block will be non-local to it, i.e. will represent the same entity inside the block and in the level immediately outside it. A label separated by a colon from a statement, i.e. labelling that statement, behaves as though declared in the head if the smallest embracing block, i.e. the smallest block whose brackets begin and end enclose that statement.
A label is said to be implicitly declared in this block head, as distinct from the explicit declaration of all other local identifiers. In this context a procedure body, or the statement following a for clause, must be considered as if it were enclosed by begin and end and treated as a block, this block being nested within the fictitious block of Section 4.7.3.1, in the case of a procedure with parameters by value. A label that is not within any block of the program (nor with a procedure body, or the statement following a for clause) is implicitly declared in the head of the environmental block.
Since a statement of a block may again itself be a block the concepts local and non-local to a block must be understood recursively. Thus an identifier which is non-local to a block A, may or may not be non-local to the block B in which A is one statement.
<destination> ::= <variable> | <procedure identifier>
<left part> ::= <destination> :=
<left part list> ::= <left part> | <left part list> <left part>
<assignment statement> ::= <left part list> <arithmetic expression> |
<left part list> <Boolean expression>
s := p[0] := n := n + 1 + s n := n + 1 A := B/C - v - q
4.2.3. Semantics
Assignment statements serve for assigning the value of an expression to one or several destinations.
Assignment to a procedure identifier may only occur within the body of a procedure defining the
value of the function designator denoted by that identifier (see Section 5.4.4). If assignment is made to a subscripted variable, the values of all the subscripts must lie within the appropriate subscript
bounds. Otherwise the action of the program becomes undefined.
The process will in the general case be understood to take place in three steps as follows:
4.2.3.1. Any subscript expressions occurring in the destinations are evaluated in sequence from left to right.
4.2.3.2. The expression of the statement is evaluated.
4.2.3.3. The value of the expression is assigned to all the destinations, with any subscript expres-sions having values as evaluated in step 4.2.3.1.
4.2.4. Types
The type associated with all destinations of a left part list must be the same. If this type is Boolean,
the expression must likewise be Boolean. If the type is real or integer, the expression must be arithmetic.
If the type of the arithmetic expression differs from that associated with the destinations, an
appropriate transfer function is understood to be automatically invoked. For transfer from real to
integer type the transfer function is understood to yield a result which is the largest integral quantity
not exceeding E + 0.5 in the mathematical sense (i.e. without rounding error) where E is the value
of the expression. It should be noted that E, being of real type, is defined with only finite accuracy
(see Section 3.3.6). The type associated with a procedure identifier is given by the declarator which
appears as the first symbol of the corresponding procedure declaration (see Section 5.4.4).
<go to statement> ::= go to <designational expression>
go to L8 go to exit[n + 1] go to Town[if y < 0 then N else N + 1] go to if Ab < c then L17 else q [if w < 0 then 2 else n]
4.3.3. Semantics
A go to statement interrupts the normal sequence of operations, by defining its successor explicitly
by the value of a designational expression. Thus the next statement to be executed will be the one
having this value as its label.
4.3.4. Restriction
Since labels are inherently local, no go to statement can lead from outside into a block. A go to
statement may, however, lead from outside into a compound statement.
4.3.5. Go to an undefined switch designator
A go to statement is undefined if the designational expression is a switch designator whose value is
undefined.
<dummy statement> ::= <empty>
L: begin statements; John: end
4.4.3. Semantics
A dummy statement executes no operation. It may serve to place a label.
<if clause> ::= if <Boolean expression> then
<unconditional statement> ::= <basic statement> |
<compound statement> | <block>
<if statement> ::= <if clause> <unconditional statement>
<conditional statement> ::= <if statement> |
<if statement> else <statement> |
<if clause> <for statement> |
<block>: <conditional statement>
if x > 0 then n := n + 1 if v > u then V: q := n + m else go to R if s < 0
4.5.3. Semantics
Conditional statements cause certain statements to
be executed or skipped depending on the running values of specified
Boolean expressions.
4.5.3.1. If statement
An if statement is of the form
if B then Su
where B is a Boolean expression and Su is an unconditional statement. In execution, B is evaluated;
if the result is true, Su is executed; if the result is false, Su is not executed.
If Su contains a label, and a go to statement leads to the label, then B is not evaluated, and the
computation continues with execution of the labelled statement.
4.5.3.2. Conditional statement
Three forms of unlabelled conditional statements exist, namely:
if B then Su if B then Sfor if B then Su else S
where Su is an unconditional statement, for is a for statement, and S is a statement.
The meaning of the first form is given in Section 4.5.3.1.
The second form is equivalent to
if B then begin Sfor end
The third form is equivalent to
begin if B then begin Su; go to G end;
(For the use of see Section 2.1 Letters.) If S is conditional and also of this form, a different label
must be used instead of following the same rule.
4.5.4. Go to into a conditional statement
The effect of a go to statement leading into a conditional statement follows directly from the above
explanation of the execution of conditional statement..
<for list element> ::= <arithmetic expression> |
<arithmetic expression> step <arithmetic expression>
until <arithmetic expression> |
<arithmetic expression> while <Boolean expression>
<for list> ::= <for list element> | <for list> ,
<for list element>
<for clause> ::= for <variable> := <for list> do
<for statement> ::= <for clause> <statement> |
<label>: <for statement>
for q := 1 step s until n do A[q] := B[q] for k := 1, V1
4.6.3. Semantics
A for clause causes the statement S which it precedes
to be repeatedly executed zero or more times. In addition it performs a
sequence of assignments to its controlled variable (the variable after for).
The controlled variable must be of real or integer type.
4.6.4. The for list elements
If the for list contain more than one element then
for V := X, Y do S
where X is a for list element, and Y is a for list (which may consist of one element or more), is equivalent to
begin
procedure S; S;
for V := X do ;
for V := Y do
end
(For the use of see Section 2.1 Letters.)
4.6.4.1. Arithmetic expression
If X is an arithmetic expression then
for V := X do S
is equivalent to
begin
V := X; S
end
where S is treated as if it were a block (see Section 4.1.3).
4.6.4.2. Step-until element
If A, B, and C are arithmetic expressions then
for V := A step B until C do S
is equivalent to
begin <type of B>
where S is treated as if it were a block (see Section 4.1.3).
In the above, <type of B> must be replaced by real or integer according to the type of B. (For
the use of and see Section 2.1 Letters.)
4.6.4.3. While element
If E is an arithmetic expression and F is a Boolean expression then
for V := E while F do S
is equivalent to
begin
where both S and the outermost compound statement of the above expansion are treated as if they
were blocks (see Section 4.1.3). (For the use of see Section 2.1 Letters.)
4.6.5. The value of the controlled variable upon exit
Upon exit from the for statement, either through a go to statement, or by exhaustion of the for list,
the controlled variable retains the last value assigned to it.
4.6.6. Go to leading into a for statement
The statement following a for clause always acts like a block, whether it has the form of one or not.
Consequently the scope of any label within this statement can never extend beyond the statement.
<actual parameter> ::= <string> | <expression> |
<array identifier> | <switch identifier> | <procedure identifier>
<letter string> ::= <letter> | <letter string> <letter>
<parameter delimiter> ::= , | ) <letter string> : (
<actual parameter list> ::= <actual parameter> |
<actual parameter list> <parameter delimiter> <actual parameter>
<actual parameter part> ::= <empty> | ( <actual parameter list> )
<procedure statement> ::= <procedure identifier> <actual parameter part>
Spur(A) Order:(7) Result to:(V) Transpose(W, v + 1) Absmax(A, N, M, Yy, I, K) Innerproduct(A[t, P, u], B[P], 10, P, Y)
These examples correspond to examples given in Section 5.4.2.
4.7.3. Semantics
A procedure statement serves to invoke (call for) the execution of a procedure body (see Section 5.4 Procedure declarations).
Where the procedure body is a statement written in ALGOL the effect of
this execution will be equivalent to the effect of performing the following operations on the program
at the time of execution of the procedure statement:
4.7.3.1. Value assignment (call by value)
All formal parameters quoted in the value part of the procedure heading (see Section 5.4) are assigned
the values (see Section 2.8 Values and types) of the corresponding actual parameters, these
assignments being considered as being performed explicitly before entering the procedure body. The
effect is as though an additional block embracing the procedure body were created in which these
assignments were made to variables local to this fictitious block with types as given in the corresponding
specifications (see Section 5.4.5). As a consequence, variables called by value are to be
considered as non-local to the body of the procedure, but local to the fictitious block (see Section 5.4.3).
4.7.3.2. Name replacement (call by name)
Any formal parameter not quoted in the value list is replaced, throughout the procedure body, by
the corresponding actual parameter, after enclosing this latter in parentheses if it is an expression
but not a variable. Possible conflicts between identifiers inserted through this process and other
identifiers already present within the procedure body will be avoided by suitable systematic changes
of the formal or local identifiers involved.
If the actual and formal parameters are of different arithmetic types, then the appropriate type conversion must take place, irrespective of the context of use of the parameter.
4.7.3.3. Body replacement and execution
Finally the procedure body, modified as above, is inserted in place of the procedure statement and
executed. If the procedure is called from a place outside the scope of any non-local quantity of the
procedure body the conflicts between identifiers inserted through this process of body replacement
and the identifiers whose declarations are valid at the place of the procedure statement or function
designator will be avoided through suitable systematic changes of the latter identifiers.
4.7.4. Actual-formal correspondence
The correspondence between the actual parameters of the procedure statement and formal parameters
of the procedure heading is established as follows: The actual parameter list of the procedure
statement must have the same number of entries as the formal parameter list of the procedure declaration
heading. The correspondence is obtained by taking the entries of these two lists in the same
order.
4.7.5. Restrictions
For a procedure statement to be defined it is evidently necessary that the operations on the procedure
body defined in Sections 4.7.3.1 and 4.7.3.2 lead to a correct ALGOL statement.
This imposes the restriction on any procedure statement that the kind and type of each actual parameter be compatible with the kind and type of the corresponding formal parameter. Some important particular cases of this general rule, and some additional restrictions, are the following:
4.7.5.1. If a string is supplied as an actual parameter in a procedure statement or function designator, whose defining procedure body is an Algol 60 statement (as opposed to non-Algol code, see Section 4.7.8), then this string can only be used within the procedure body as an actual parameter in further procedure calls. Ultimately it can only be used by a procedure body expressed in non-Algol code.
4.7.5.2. A formal parameter which occurs as a left part variable in an assignment statement within the procedure body and which is not called by value can only correspond to an actual parameter which is a variable (special case of expression).
4.7.5.3. A formal parameter which is used within the procedure body as an array identifier can only correspond to an actual parameter which is an array identifier of an array of the same dimensions. In addition if the formal parameter is called by value the local array created during the call will have the same subscript bounds as the actual array.
Similarly the number, kind and type of any parameter of a formal procedure parameter must be compatible with those of the actual parameter.
4.7.5.4. A formal parameter which is called by value cannot in general correspond to a switch identifier or a procedure identifier or a string, because latter do not posses values (the exception is the procedure identifier of a procedure declaration which has an empty formal parameter part (see Section 5.4.1) and which defines the value of a function designator (see Section 5.4.4). This procedure identifier is in itself a complete expression).
4.7.5.5. Restrictions imposed by specifications of formal parameters must be observed. The correspondence between actual and formal parameters should be in accordance with the following table.
| Formal parameter | Mode | Actual parameter |
| integer | value | arithmetic expression |
| name | arithmetic expression (see 4.7.5.2) | |
| real | value | arithmetic expression |
| name | arithmetic expression (see 4.7.5.2) | |
| Boolean | value | Boolean expression |
| name | Boolean expression (see 4.7.5.2) | |
| label | value | designational expression |
| name | designational expression | |
| integer array | value | arithmetic array (see 4.7.5.3) |
| name | integer array (see 4.7.5.3) | |
| real array | value | arithmetic array (see 4.7.5.3) |
| name | real array (see 4.7.5.3) | |
| Boolean array | value | Boolean array (see 4.7.5.3) |
| name | Boolean array (see 4.7.5.3) | |
| typeless procedure | name | arithmetic procedure, or typeless procedure, or Boolean procedure (see 4.7.5.3) |
| integer procedure | name | arithmetic procedure (see 4.7.5.3) |
| real procedure | name | arithmetic procedure (see 4.7.5.3) |
| Boolean procedure | name | Boolean procedure (see 4.7.5.3) |
| switch | name | switch |
| string | name | actual string or string identifier |
If the actual parameter is itself a formal parameter the correspondence (as in the above table) must be with the specification of the immediate actual parameter rather than with the declaration of the ultimate actual parameter.
4.7.6. Label parameters
A label may be called by value, even though variables of type label do not exist.
4.7.7. Parameter delimiters
All parameter delimiters are understood to be equivalent. No correspondence between the parameter
delimiters used in a procedure statement and those used in the procedure heading is expected beyond
their number being the same. Thus the information conveyed by using the elaborate ones is
entirely optional.
4.7.8. Procedure body expressed in code
The restrictions imposed on a procedure statement calling a procedure having its body expressed in
non-ALGOL code evidently can only be derived from the characteristics of the code used and the
intent of the user and thus fall outside the scope of the reference language.
4.7.9. Standard procedures
Ten standard procedures are defined, which are declared in the environmental block in an identical
manner to the standard functions. These procedures are: inchar, outchar, outstring, ininteger, inreal,
outinteger, outreal, outterminator, fault and stop. The input/output procedures identify physical
devices or files by means of channel numbers which appear as the first parameter. The method by
which this identification is achieved is outside the scope of this report. Each channel is regarded as
containing a sequence of characters; basic method of accessing or assigning these characters being
via the procedures inchar and outchar.
The procedures inreal and outreal are converses of each other in the sense that a channel containing characters from successive calls of outreal can be re-input by the same number of calls of inreal, and some accuracy may be lost. The procedures ininteger and outinteger are also a pair, but no accuracy can be lost. The procedure outterminator is called at the end of each of the procedure outreal and outinteger. Its action is machine dependent but it must ensure separation between successive output of numeric data.
Possible implementation of these additional procedures are given in Appendix 2 as examples to illustrate the environmental block.
Declarations serve to define certain properties of the quantities used in the program, and to associate them with identifiers. A declaration of an identifier is valid for one block. Outside this block the particular identifier may be used for other purposes (see Section 4.1.3).
Dynamically this implies the following: at the time of an entry into a block (through begin since the labels inside are local and therefore inaccessible from outside) all identifiers declared for the block assume the significance implied by the nature of the declarations given. If these identifiers had already been defined by other declarations outside they are for the time being given a new significance. Identifiers which are not declared for the block, on the other hand, retain their old meaning.
At the the time of an exit from a block (through end, or by a go to statement) all identifiers which are declared for the block lose their local significance.
A declaration may be marked with additional declarator own. This has the following effect: upon a reentry into the block, the values of own quantities will be unchanged from their values at the last exit, while the values of declared variables which are not marked as own are undefined.
Apart from labels, formal parameters of procedure declarations and identifiers declared in the environmental block, each identifier appearing in a program must be explicitly declared within a program.
No identifier may be declared either explicitly or implicitly (see Section 4.1.3) more than once in any one block head.
Syntax
<declaration> ::= <type declaration> | <array declaration> |
<switch declaration> | <procedure declaration>
<type list> ::= <simple variable> | <simple variable> , <type list> <type> ::= real | integer | Boolean <local or own> ::= <empty> | own <type declaration> ::= <local or own> <type> <type list>
integer p, q, s own Boolean Acryl, n
5.1.3. Semantics
Type declarations serve to declare certain identifiers to represent simple variables of a given type.
Real declared variables may only assume positive or negative values including zero. Integer declared
variables may only assume positive and negative integral values including zero. Boolean declared
variables may only assume the values true and false.
A variable declared own behaves as if it had been declared (and initialised to zero or false, see Section 3.1.5) in the environmental block, except that it is accessible only within its own scope. Possible conflicts between identifiers, resulting from this process, resolved by suitable systematic changes of the identifiers involved.
<lower bound> ::= <arithmetic expression>
<upper bound> ::= <arithmetic expression>
<bound pair> ::= <lower bound> : <upper bound>
<bound pair list> ::= <bound pair> |
<bound pair list> , <bound pair>
<array segment> ::= <array identifier> [ <bound pair list> ] |
<array identifier> , <array segment>
<array list> ::= <array segment> |
<array list> , <array segment>
<array declarer> ::= <type> array | array
<array declaration> ::= <local or own> <array declarer> <array list>
array a, b, c[7:n, 2:m], s[-2:10] own integer array A[2:20] real array q [-7: if c < 0 then 2 else 1]
5.2.3. Semantics
An array declaration declares one or several identifiers to represent multidimensional arrays of subscripted
variables and gives the dimensions of the arrays, the bounds of the subscripts, and the
types of the variables.
5.2.3.1. Subscript bounds
The subscript bounds for any array are given in the first subscript brackets following the identifier
of this array in the form of a bound pair list. Each item of this list gives the lower and upper bounds
of a subscript in the form of two arithmetic expressions separated by the delimiter :. The bound pair
list gives the bounds of all subscripts taken in order from left to right.
5.2.3.2. Dimensions
The dimensions are given as the number of entries in the bound pair lists.
5.2.3.3. Types
All arrays declared in one declaration are of the same quoted type. If no type declarator is given the
real type is understood.
5.2.4. Lower upper bound expressions
5.2.4.1. The expressions will be evaluated in the same way as subscript expression (see Section 3.1.4.2).
5.2.4.2. The expressions cannot include any identifier that is declared, either explicitly or implicitly (see Section 4.1.3), in the same block head as the array in question. The bounds of an array declared as own may only be of the syntactic form integer (see Section 2.5.1).
5.2.4.3. An array is defined only when the values of all upper subscript bounds are not smaller than those of the corresponding lower bounds. If any lower subscript bound is greater that the corresponding upper bound, the array has no component.
5.2.4.4. The expressions will be evaluated once at each entrance into the block.
<switch list> ::= <designational expression> |
<switch list> , <designational expression>
<switch declaration> ::= switch <switch identifier> := <switch list>
switch S := S1, S2, Q[m], if v > -5 then S3 else S4 switch Q := p1, w
5.3.3. Semantics
A switch declaration defines the set of values of the corresponding switch designators. These values
are given one by one as the values of the designational expressions entered in the switch list. With
each of these designational expressions there is associated a positive integer, 1, 2, . . ., obtained by counting the items in the list from left to right. The value of the switch designator corresponding to
a given value of the subscript expression (see Section 3.5 Designational expressions) is the value of the designational expression in the switch list having this given value as its associated integer.
5.3.4. Evaluation of expressions in the switch list
An expression in the switch list will be evaluated every time the item of the list in which the expression
occurs is referred to, using the current values of all variables involved.
5.3.5. Influence of scopes
If a switch designator occurs outside the scope of a quantity entering into a designational expression
in the switch list, and an evaluation of this switch designator selects this designational expression,
then the conflicts between the identifiers for the quantities in this expression and the identifiers
whose declarations are valid at the place of the switch designator will be avoided through suitable
systematic changes of the latter identifiers.
<formal parameter> ::= <identifier>
<formal parameter list> ::= <formal parameter> |
<formal parameter list> <parameter delimiter> <formal parameter>
<formal parameter part> ::= <empty> | ( <formal parameter list> )
<identifier list> ::= <identifier> |
<identifier list> , <identifier>
<value part> ::= value <identifier list> ; | <empty>
<specifier> ::= string | <type> | <array declarer> |
label | switch | procedure | <type> procedure
<specification part> ::= <empty> | <specifier> <identifier list> ; |
<specification part> <specifier> <identifier list>
<procedure heading> ::= <procedure identifier> <formal parameter part> ;
<value part> <specification part>
<procedure body> ::= <statement> | <code>
<procedure declaration> ::= procedure <procedure heading> <procedure body> |
<type> procedure <procedure heading> <procedure body>
5.4.2. Examples (see also the examples in Appendix 2)
procedure Spur(a) Order:(n) Result:(s); value n;
array a; integer n; real s;
begin integer k;
s := 0;
for k := 1 step 1 until n do s := s + a[k, k]
end
procedure Transpose(a) Order:(n); value n;
array a; integer n;
begin real w; integer i, k;
for i := 1 step 1 until n do
for k := 1 + i step 1 until n do
begin w := a[i, k];
a[i, k] := a[k, i];
a[k, i] := w
end
end Transpose
integer procedure Step(u); real u;
Step := if 0 u u 1 then 1 else 0
procedure Absmax(a) Size:(n, m) Result:(y) Subscripts:(i, k);
value n, m; array a; integer n, m, i, k; real y;
comment The absolute greatest element of the matrix a, of size n by m
is transferred to y, and the subscripts of this element to i and k;
begin integer p, q;
y := 0; i := k := 1;
for p:=1 step 1 until n do
for q:=1 step 1 until m do
if abs(a[p, q]]) > y then
begin y :=a bs(a[p, q]);
i := p; k := q
end
end Absmax
procedure Innerproduct(a, b) Order:(k, p) Result:(y); value k;
integer k, p; real y, a, b;
begin real s;
s := 0;
for p := 1 step 1 until k do s := s + a b;
y := s
end Innerproduct
real procedure euler(fct, eps, tim);
value eps, tim;
real procedure fct; real eps; integer tim;
comment euler computes the sum of fct(i) for i from zero up to
infinity by means of a suitably refined euler transformation. The summation
is stopped as soon as tim times in succession the absolute value of the
terms of the transformed series are found to be less than eps.
Hence one should provide a function fct with one integer argument, an upper
bound eps, and an integer tim. euler is particularly efficient in the case
of a slowly convergent or divergent alternating series;
begin
integer i, k, n, r;
array m[0:15];
real mn, mp, ds, sum;
n := t := 0;
m[0] := fct(0); sum := m[0]/2;
for i := 1, i + 1 while t < tim do
begin
mn := fct(i);
for k := 0 step 1 until n do
begin
mp := (mn + m[k])/2;
m[k] := mn; mn := mp
end means;
if abs(mn) < abs(m[n]) n < 15 then
begin
ds := mn/2; n := n + 1;
m[n] := mn
end accept
else
ds := mn;
sum := sum + ds;
t := if abs(ds) < eps then t + 1 else 0
end;
euler := sum
end euler
5.4.3. Semantics
A procedure declaration serves to define the procedure associated with a procedure identifier. The
principal constituent of a procedure declaration is a statement or a piece of code, the procedure
body, which through the use of procedure statements and/or function designators may be activated
from other parts of the block in the head of which the procedure declaration appears. Associated
with the body is a heading, which specifies certain identifiers occurring within the body to represent
formal parameters. Formal parameters in the procedure body will, whenever the procedure is activated
(see Section 3.2 Function designators and Section 4.7 Procedure statements) be assigned the
values of or replaced by actual parameters. Identifiers in the procedure body which are not formal
will be wither local or non-local to the body depending on whether they are declared within the
body or not. Those of them which are non-local to the body may well be local to the block in the
head of which the procedure declaration appears. The procedure body always acts like a block,
whether it has the form of one or not. Consequently the scope of any label labelling a statement
within the body or the body itself can never extend beyond the procedure body. In addition, if the
identifier of a formal parameter is declared anew within the procedure body (including the case of
its use as a label as in Section 4.1.3), it is hereby given a local significance and actual parameters
which correspond to it are inaccessible throughout the scope of this inner local quantity.
No identifier may appear more than once in any one formal parameter list, nor may a formal parameter list contain the procedure identifier of the same procedure heading.
5.4.4. Values of function designators
For a procedure declaration to define the value of a function designator there must, within the procedure
body, occur one or more use of the procedure identifier as a destination; at least one of these
must be executed, and the type associated with the procedure identifier must be declared through
the appearance of a type declarator as the very first symbol of the procedure declaration. The last
value so assigned is used to continue the evaluation of the expression in which the function designator
occurs. Any occurrence of the procedure identifier within the body of the procedure other
than as a destination in an assignment statement denotes activation of the procedure.
If a go to statement within the procedure, or within any other procedure activated by it, leads to an exit from the procedure, other than through its end, then the execution, of all statements that has been started but not yet completed and which do not contain a label to which the go to statements leads, is abandoned. The values of all variables that still have significance remain as they were immediately before execution of the go to statement.
If a function designator is used as a procedure statement, then the resulting value is discarded, but such a statement may be used, if desired, for the purpose of invoking side effects.
5.4.5. Specifications
The heading includes a specification part, giving information about the kinds and types of the formal
parameters. In this part no formal parameter may occur more than once.
5.4.6. Code as procedure body.
It is understood that the procedure body may be expressed in non-ALGOL language. Since it is
intended that the use of this feature should be entirely a question of implementation, no further rules
concerning this code language can be given within the reference language.
Two subsets of ALGOL 60 are defined, denoted as level 1 and level 2. The full language is level 0.
The level 1 subset is defined as level 0 with the following additional restrictions:
| 1. | The own declarator is not included. | ||||||||||||||||||||||||
| 2. | Additional restrictions are placed upon actual parameters as given by the following replacement lines to the table in Section 4.7.5.5. | ||||||||||||||||||||||||
| |||||||||||||||||||||||||
| 3. | Only one alphabet of 26 letters is provided, which is regarded of being the lower case alphabet of the reference language. | ||||||||||||||||||||||||
| 4. | If deleting every symbol after the twelfth in every identifier would change the action of the program, then the program is undefined. |
The level 2 subset consists of 1-3 of level 1 and in addition:
| 5. | Procedures may not be called recursively, either directly or indirectly. |
| 6. | If a parameter is called by name, then the corresponding actual parameter may only be an identifier or a string. |
| 7. | The designational expressions occurring in a switch list may only be lables. |
| 8. | The specifiers switch, procedure and <type> procedure are not included. |
| 9. | A left part list may only be a left part. |
| 10. | If deleting every symbol after the sixth in every identifier would change the action of the program, then the program is undefined. |
As an example of the use of ALGOL 60, the structure of the environmental block is given in detail.
begin
comment This description of the standard functions and procedures
should be taken as definitive only so far as their effects are
concerned. An actual implementation should seek to produce these
effects in as efficient a manner as practicable. Furthermore, where
arithmetic of real quantities are concerned, even the effects must
be regarded as defined with only a finite accuracy (see Section 3.3.6).
Thus, for example, there is no guarantee that the value of sqrt(x)
is exactly equal to the value x0.5, or that the effects of inreal
and outreal will exactly match those given here.
ALGOL coding has been replaced by a metalingustic variable (see
Section 1.1) in places where the requirement is clear, and there is
no simple way of specifying the operations needed in ALGOL;
comment Simple functions;
real procedure abs(E);
value E; real E;
abs := if E 0.0 then E else -E;
integer procedure iabs(E);
value E; integer E;
iabs := if E 0 then E else -E;
integer procedure sign(E);
value E; real E;
sign := if E > 0.0 then 1
else if E < 0.0 then -1 else 0;
integer procedure entier(E);
value E; real E;
comment entier := largest integer not greater than E,
i.e. E - 1 < entier E;
begin
integer j;
j := E;
entier := if j > E then j - 1 else j
end entier;
comment Mathematical functions;
real procedure sqrt(E);
value E; real E;
if E < 0.0 then
fault(`negativesqrt', E)
else
sqrt := E0.5;
real procedure sin(E);
value E; real E;
comment sin := sine of E radians;
<body>;
real procedure cos(E);
value E; real E;
comment cos := cosine of E radians;
<body>;
real procedure arctan(E);
value E; real E;
comment arctan := principal value, in radians, of arctangent
of E, i.e. -π/2 arctan π/2;
<body>;
real procedure ln(E);
value E; real E;
comment ln := natural logarithm of E;
if E 0.0 then
fault(`lnnotpositive', E)
else
<statement>;
real procedure exp(E);
value E; real E;
comment exp := exponential function of E;
if E > ln(maxreal) then
fault(`overflowonexp', E)
else
<statement>;
comment Terminating procedures;
procedure stop;
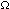comment for the use of , see Section 2.1 Letters;
go to ;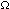
procedure fault(str, r);
value r; string str; real r;
comment is assumed to denote a standard output channel.
For the use of see Section 2.1 Letters.
The following calls of fault appear:
integer divide by zero,
undefined operation in expr,
undefined operation in expn,
undefined operation in expi,
and in the environmental block:
sqrt of negative argument,
ln of negative or zero argument,
overflow on exp function,
invalid parameter for outchar,
invalid character in ininteger (twice),
invalid character in inreal (three times);
begin
outstring(, `fault');
outstring(, str);
outstring(, `');
outreal(, r);
comment additional diagnostics may be output here;
stop
end fault;
comment Input/output procedures;
procedure inchar(channel, str, int);
value channel;
integer channel, int; string str;
comment Set int to value corresponding to the first position in
str of current character on channel. Set int to zero if character
not in str. Move channel pointer to next character;
<body>;
procedure outchar(channel, str, int);
value channel, int;
integer channel, int; string str;
comment Pass to channel the character in str, corresponding to
the value of int;
if int < 1 int > length(str) then
fault(`characternotinstring', int)
else
<statement>;
integer procedure length(str);
string str;
comment length := number of characters in the open string
enclosed by the outermost string quotes, after performing any
necessary concatenation as defined in Section 2.6.3. Characters
forming an inner string (see Section 2.6.3) are counted in an
implementation dependent manner;
<body>;
procedure outstring(channel, str);
value channel;
integer channel; string str;
begin
integer m, n;
n := length(str);
for m := 1 step 1 until n do
outchar(channel, str, m)
end outstring;
procedure outterminator(channel);
value channel; integer channel;
comment outputs a terminator for use after a number. To be
converted into format control instructions in a machine
dependent fashion. The terminator should be a space, a newline
or a semicolon if ininteger and inreal are to be able to read
representations resulting from outinteger and outreal;
<body>;
procedure ininteger(channel, int);
value channel; integer channel, int;
comment int takes the value of an integer, as defined in
Section 2.5.1, read from channel. The terminator of the
integer may be either a space, a newline or a semicolon
(if other terminators are to be allowed, they may be added
to the end of the string parameter of the call of inchar.
No other change is necessary). Any number of spaces or
newlines may precede the first character of the integer;
begin
integer k, m;
Boolean b, d;
integer procedure ins;
begin
integer n;
comment read one character, converting newlines to spaces.
The inner string `NL' behaves as a single character repre-
senting newline;
inchar(channel, `0123456789-+;`NL'', n);
ins := if n = 15 then 13 else n
end ins;
comment pass over initial spaces or newlines;
for k := ins while k = 13 do
;
comment fault anything except sign or digit;
if k = 0 k > 13 then
fault(`invalidcharacter', k);
if k > 10 then
begin
comment sign found, d indicates digit not found yet, b
indicates whether + or -, m is value so far;
d := b := true;
m := k - 1
end;
for k := ins while k > 0 k < 11 do
begin
comment deal with further digits;
m := 10 m + k - 1;
d := true
end k loop;
comment fault if no digit has been found, or the terminator
was invalid;
if d k < 13 then
fault(`invalidcharacter', k);
int := if b then m else -m
end ininteger;
procedure outinteger(channel, int);
value channel, int;
integer channel, int;
comment Passes to channel the characters representing the value
of int, followed by a terminator;
begin
procedure digits(int);
value int; integer int;
begin
integer j;
comment use recursion to evaluate digits from right to left,
but print them from left to right;
j := int ÷ 10;
int := int - 10 j;
if j 0 then
digits(j);
outchar(channel, `0123456789', int + 1)
end digits;
if int < 0 then
begin
outchar(channel, `-', 1);
int := -int
end;
digits(int); outterminator(channel)
end outinteger;
procedure inreal(channel, re);
value channel;
integer channel; real re;
comment re takes the value of a number, as defined in
Section 2.5.1, read from channel. Except for the different
definitions of a number and an integer the rules are exactly
as for ininteger. Spaces or newlines may follow the symbol 10;
begin
integer j, k, m;
real r, s;
Boolean b, d;
integer procedure ins;
begin
integer n;
comment read one character, converting newlines to spaces.
The inner string `NL' behaves as a single character repre-
senting newline;
inchar(channel, `0123456789-+.10;`NL'', n);
ins := if n = 17 then 15 else n
end ins;
comment pass over initial spaces or newlines;
for k := ins while k = 15 do
;
comment fault anything except sign, digit, point or ten;
if k = 0 k > 15 then
fault(`invalidcharacter', k);
comment b indicates whether + or -, d indicates whether further
digits can have any effect, m will count places after the point,
r is the value so far. j indicates whether last character read
was sign (j = 1), digit before point (j = 2), point (j = 3),
digit after point (j = 4), or ten (j = 5);
b := k 11;
d := true;
m := 1;
j := if k < 11 then 2 else iabs(k + k - 23);
r := if k < 11 then k - 1 else 0.0;
if k 14 then
begin
comment ten not found. Continue until ten or terminator found;
for k := ins while k < 14 do
begin
comment fault for non-numerical character, sign or second
point;
if k = 0 k = 11 k = 12
k = 13 j > 2 then
fault(`invalidcharacter', k);
comment deal with digit unless it cannot affect value;
if d then
begin
if k = 13 then
begin
comment point found;
j := 3
end
else
begin
if j < 3 then
begin
comment deal with digit before point;
r := 10.0 r + k - 1
end
else
begin
comment deal with digit after point;
s := 10.0(-m);
m := m + 1;
r := r + s (k - 1);
comment if r = r + s to machine accuracy,
further digits cannot affect value;
d := r r + s
end;
if j = 1 j = 3 then j := j + 1
end
end
end k loop;
comment fault if no digit has been found;
if j = 1 k 14 j = 3 then
fault(`invalidcharacter', k);
end;
if k = 14 then
begin
comment deal with exponent part;
ininteger(channel, m);
r := (if j = 1 j = 5 then 1.0 else r) 10.0m
end;
re := if b then r else - r
end inreal;
procedure outreal(channel, re);
value channel, re;
integer channel; real re;
comment Passes to channel the characters representing the value of
re, following by a terminator;
begin
integer n;
comment n gives number of digits to print. Could be given as a
constant in any actual implementation;
n := entier(1.0 - ln(epsilon) / ln(10.0));
if re < 0.0 then
begin
outchar(channel, `-', 1);
re := - re
end;
if re < minreal then
outstring(channel, 0.0 )
else
begin
integer j, k, m, p;
Boolean float, nines;
comment m will hold number of places point must be moved to
standardise value of re to have one digit before point;
m := 0;
comment standardise value of re;
for m := m + 1 while re 10.0 do
re := re/10.0;
for m := m - 1 while re < 1.0 do
re := 10.0 re;
if re 10.0 then
begin
comment this can occur only by rounding error, but is a
necessary safeguard;
re := 1.0;
m := m + 1
end;
if m n m < -2 then
begin
comment printing to be in exponent form;
float := true;
p := 1
end
else
begin
comment printing to be in non-exponent form;
float := false;
comment if p = 0 point will not be printed. Otherwise
point will be after p digits;
p := if m = n - 1 m < 0 then 0 else m + 1;
if m < 0 then
begin
outstring(channel, `0.');
if m = -2 then
outchar(channel, `0', 1)
end
end;
nines := false;
for j := 1 step 1 until n do
begin
comment if nines is true, all remaining digits must
be 9. This can occur only by rounding error, but is
a necessary safeguard;
if nines then
k := 9
else
begin
comment find digit to print;
k := entier(re);
if k > 9 then
begin
k := 9;
nines := true
end
else
begin
comment move next digit to before point;
re := 10.0 (re - k)
end
end;
outchar(channel, `0123456789', k + 1);
if j = p then
outchar(channel, `.', 1)
end j loop;
if float then
begin
comment print exponent part. outinteger includes a call
of outterminator;
outchar(channel, `10 , 1);
outinteger(channel, m)
end
else
outterminator(channel)
end
end outreal;
comment Environmental enquiries;
real procedure maxreal;
maxreal := <number>;
real procedure minreal;
minreal := <number>;
integer procedure maxint;
maxint := <integer>;
comment maxreal, minreal, and maxint are, respectively, the maximum
allowable positive real number, the minimum allowable positive real
number, and the maximum allowable positive integer, such that any
valid expression of the form
<primary> <arithmetic operator> <primary>
will be correctly evaluated, provided that each of the primaries
concerned, and the mathematically correct result lies within the
open interval (-maxreal, -minreal) or (minreal, maxreal) or is zero
if of real type, or within the open interval (-maxint, maxint) if
of integer type. If the result is of real type, the words
`correctly evaluated' must be understood in the sense of numerical
analysis (see Section 3.3.6);
real procedure epsilon;
comment The smallest positive real number such that the
computational result of 1.0 + epsilon is greater than 1.0 and
the computational result of 1.0 - epsilon is less than 1.0;
epsilon := <number>;
comment In any particular implementation, further standard functions
and procedures may be added here, but no additional ones may be
regarded as part of the reference language (in particular, a less
rudimentary input/output system is desirable);
<fictitious declaration of own variables>;
<initialisation of own variables>;
<program>;
:
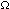end
| BACKUS, J. W. (1959) | ||
| The syntax and Semantics of the Proposed International Algebraic Language. Information Processing, Paris, UNESCO. | ||
| ECMA Subset of ALGOL 60 | ||
| CACM, Vol, 6 (1963), p. 595; European Computer Manufacturers Association (1965) ECMA Standard for a Subset of ALGOL 60. | ||
| IFIP (1964a) | ||
| Report on Subset ALGOL 60, Num. Math., Vol. 6, p. 454; CACM, Vol. 7, p. 626. | ||
| IFIP (1964b) | ||
| Report on Input-Output Procedures for ALGOL 60, Num. Math., Vol. 6, p. 459; CACM, Vol. 7, p. 628. | ||
| ISO (1972) | ||
| ISO/R 1538, Programming Language ALGOL. | ||
| KNUTH, D. E. et al. (1964) | ||
| A Proposal for Input-Output Conventions in ALGOL 60, CACM, Vol. 7, p. 273. | ||
| KNUTH, D. E. (1967) | ||
| The Remaining Trouble Spots in ALGOL 60, CACM, Vol. 10, p. 611. | ||
| NAUR, P. (Editor) (1963) | ||
| Revised Report on the Algorithmic Language ALGOL 60, CACM, Vol. 6, p. 1; The Computer Journal, Vol. 9, p. 349; Num. Math., Vol. 4, p. 420. | ||
| UTMAN, R. E. et al. (1963) | ||
| Suggestions on the ALGOL 60 (Rome) Issues, CACM, Vol. 6, p. 20. | ||
All references are given through section numbers.
The references are given in three groups:
| def | Following the abbreviation `def', reference to the syntactic definition (if any) is given. |
| synt | Following the abbreviation `synt', references to the occurrences in metalinguistic formulae are given. References already quoted in the def-group are not repeated. |
| text | Following the word `text', the references to definitions given in text are given. |
Index: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
+ see: plus - see: minus
<actual parameter>, def 3.2.1, 4.7.1
<actual parameter list>, def 3.2.1, 4.7.1
<actual parameter part>, def 3.2.1, 4.7.1
<adding operator>, def 3.3.1
alphabet, text 2.1
arithmetic, text 3.3.6
<arithmetic expression>, def 3.3.1 synt 3, 3.1.1, 3.4.1, 4.2.1, 4.6.1, 5.2.1 text 3.3.3
<arithmetic operator>, def 2.3 text 3.3.4
array, synt 2.3, 5.2.1
array, text 3.1.4.1
<array declaration>, def 5.2.1 synt 5 text 5.2.3
<array declarer>, def 5.2.1, synt 5.4.1
<array identifier>, def 3.1.1 synt 3.2.1, 4.7.1, 5.2.1 text 2.8
<array list>, def 5.2.1
<array segment>, def 5.2.1
<assignment statement>, def 4.2.1 synt 4.1.1 text 1, 4.2.3
<basic statement>, def 4.1.1 synt 4.5.1
<basic symbol>, def 2
begin, synt 2.3, 4.1.1
<block>, def 4.1.1 synt 4.5.1 text 1, 4.1.3, 5
<block head>, def 4.1.1
Boolean, synt 2.3, 5.1.1 text 5.1.3
<Boolean expression>, def 3.4.1 synt 3, 3.3.1, 4.2.1, 4.5.1, 4.6.1 text 3.4.3
<Boolean factor>, def 3.4.1
<Boolean primary>, def 3.4.1
<Boolean secondary>, def 3.4.1
<Boolean term>, def 3.4.1
<bound pair>, def 5.2.1
<bound pair list>, def 5.2.1
<bracket>, def 2.3
<closed string>, def 2.6.1
<code>, synt 5.4.1 text 4.7.8, 5.4.6
colon :, synt 2.3, 3.2.1, 4.1.1, 4.5.1, 4.6.1, 4.7.1, 5.2.1
colon equal :=, synt 2.3, 4.2.1, 4.6.1, 5.3.1
comma ,, synt 2.3, 3.1.1, 3.2.1, 4.6.1, 4.7.1, 5.1.1, 5.2.1, 5.3.1, 5.4.1
comment, synt 2.3
comment convention, text 2.3
<compound statement>, def 4.1.1 synt 4.5.1 text 1
<compound tail>, def 4.1.1
<conditional statement>, def 4.5.1 synt 4.1.1 text 4.5.3
<decimal fraction>, def 2.5.1
<decimal number>, def 2.5.1 text 2.5.3
decimal point ., synt 2.3, 2.5.1
<declaration>, def 5 synt 4.1.1 text 1, 5
<declarator>, def 2.3
<delimiter>, def 2.3 synt 2
<designational expression>, def 3.5.1 synt 3, 4.3.1, 5.3.1 text 3.5.3
<destination>, def 4.2.1
<digit>, def 2.2.1 synt 2, 2.4.1, 2.5.1
dimension, text 5.2.3.2
divide / &devide;, synt 2.3, 3.3.1 text 3.3.4.2
do, synt 2.3, 4.6.1
<dummy statement>, def 4.4.1 synt 4.1.1 text 4.4.3
else, synt 2.3, 3.3.1, 3.4.1, 3.5.1, 4.5.1 text 4.5.3.2
<empty>, def 1.1 synt 2.6.1, 3.2.1, 4.4.1, 4.7.1, 5.1.1, 5.4.1
end, synt 2.3, 4.1.1
exponentiation , synt 2.3, 3.3.1 text 3.3.4.3
<exponent part>, def 2.5.1 text 2.5.3
<expression>, def 3 synt 3.2.1, 4.7.1 text 3
<factor>, def 3.3.1
false, synt 2.2.2
for, synt 2.3, 4.6.1
<for clause>, def 4.6.1 text 4.6.3
<for list>, def 4.6.1 text 4.6.4
<for list element>, def 4.6.1 text 4.6.4.1, 4.6.4.2, 4.6.4.3
<formal parameter>, def 5.4.1, text 5.4.3
<formal parameter list>, def 5.4.1
<formal parameter part>, def 5.4.1
<for statement>, def 4.6.1 synt 4.1.1, 4.5.1 text 4.6
<function designator>, def 3.2.1 synt 3.3.1, 3.4.1 text 3.2.3, 5.4.4
go to, synt 2.3, 4.3.1
<go to statement>, def 4.3.1 synt 4.1.1 text 4.3.3
<identifier>, def 2.4.1 synt 3.1.1, 3.2.1, 3.5.1, 5.4.1 text 2.4.3
<identifier list>, def 5.4.1
if, synt 2.3, 3.3.1, 4.5.1
<if clause>, def 3.3.1, 4.5.1 synt 3.4.1, 3.5.1 text 3.3.3, 4.5.3.2
<if statement>, def 4.5.1 text 4.5.3.1
<implication>, def 3.4.1
integer, synt 2.3, 5.1.1 text 5.1.3
<integer>, def 2.5.1 text 2.5.4
label, synt 2.3, 5.4.1
<label>, def 3.5.1 synt 4.1.1, 4.5.1, 4.6.1 text 1, 4.1.3, 4.7.6
<left part>, def 4.2.1
<left part list>, def 4.2.1
<letter>, def 2.1 synt 2, 2.4.1, 3.2.1, 4.7.1
<letter string>, def 3.2.1, 4.7.1
local, text 4.1.2
<local or own>, def 5.1.1, synt 5.4.1
<logical operator>, def 2.3 synt 3.4.1 text 3.4.5
<logical value>, def 2.2.2 synt 2, 3.4.1
<lower bound>, def 5.2.1 text 5.2.4
minus -, synt 2.3, 2.5.1, 3.3.1 text 3.3.4.1
multiply , synt 2.3, 3.3.1 text 3.3.4.1
<multiplying operator>, def 3.3.1
non-local, text 4.1.3
<number>, def 2.5.1 text 2.5.3, 2.5.4
<open string>, def 2.6.1
<operator>, def 2.3
own, synt 2.3, 5.1.1 text 5, 5.2.5
<parameter delimiter>, def 3.2.1, 4.7.1 synt 5.4.1 text 4.7.7
parentheses ( ), synt 2.3, 3.2.1, 3.3.1, 3.4.1, 3.5.1, 4.7.1, 5.4.1, text 3.3.5.2
plus +, synt 2.3, 2.5.1, 3.3.1 text 3.3.4.1
<primary>, def 3.3.1
procedure, synt 2.3, 5.4.1
<procedure body>, def 5.4.1
<procedure declaration>, def 5.4.1 synt 5 text 5.4.3
<procedure heading>, def 5.4.1 text 5.4.3
<procedure identifier>, def 3.2.1 synt 3.2.1, 4.2.1, 4.7.1, 5.4.1 text 4.7.5.4
<procedure statement>, def 4.7.1 synt 4.1.1 text 4.7.3
<program>, def 4.1.1 text 1
<proper string>, def 2.6.1
quantity, text 2.7
real, synt 2.3, 5.1.1 text 5.1.3
<relation>, def 3.4.1 text 3.4.5
<relational operator>, def 2.3, 3.4.1
scope, text 2.7
semicolon ;, synt 2.3, 4.1.1, 5.4.1
<separator>, def 2.3
<sequential operator>, def 2.3
<simple arithmetic expression>, def 3.3.1 synt 3.4.1 text 3.3.3
<simple Boolean>, def 3.4.1
<simple designational expression>, def 3.5.1
<simple variable>, def 3.1.1 synt 5.1.1 text 2.4.3
<specification part>, def 5.4.1 text 5.4.5
<specificator>, def 2.3
<specifier>, def 5.4.1
standard functions and procedures, text 3.2.4
standard procedures, text 4.7.9
<statement>, def 4.1.1 synt 4.5.1, 4.6.1, 5.4.1 text 4
statement bracket see: begin end
step, synt 2.3, 4.6.1 text 4.6.4.2
string, synt 2.3, 5.4.1
<string>, def 2.6.1 synt 3.2.1, 4.7.1 text 2.6.3
string quotes ` ', synt 2.3, 2.6.1 text 2.6.3
subscript, text 3.1.4.1
subscript bound, text 5.2.3.1
subscript brackets [ ], synt 2.3, 3.1.1, 3.5.1, 5.2.1
<subscripted variable>, def 3.3.1 text 3.1.4.1
<subscript expression>, def 3.1.1 synt 3.5.1
<subscript list>, def 3.1.1
successor, text 4
switch, synt 2.3, 5.3.1, 5.4.1
<switch declaration>, def 5.3.1 synt 5 text 5.3.3
<switch designator>, def 3.5.1 text 3.5.3
<switch identifier>, def 5.3.1
<term>, def 3.3.1
ten 10, synt 2.3, 2.5.1
then, synt 2.3, 3.3.1, 4.5.1
true, synt 2.2.2
<type>, def 5.1.1 synt 5.4.1 text 2.8
<type declaration>, def 5.1.1 synt 5 text 5.1.3
<type list>, def 5.1.1
<unconditional statement>, def 4.1.1, 4.5.1
<unlabelled basic statement>, def 4.1.1
<unlabelled block>, def 4.1.1
<unlabelled compound>, def 4.1.1
<unsigned integer>, def 2.5.1
<unsigned number>, def 2.5.1 synt 3.3.1
until, synt 2.3, 4.6.1 text 4.6.4.2
<upper bound>, def 5.2.1 text 5.2.4
value, synt 2.3, 5.4.1
value, text 2.8, 3.3.3
<value part>, def 5.4.1 text 4.7.3.1
<variable>, def 3.1.1 synt 3.3.1, 3.4.1, 4.2.1, text 3.1.3
<variable identifier>, def 3.1.1 synt 4.6.1
while, synt 2.3, 4.6.1 text 4.6.4.3
Insofar as this Modified Report is a correct application of the Supplement to the Revised Report, reproduction for any purpose, but only of the whole text, is explicitly permitted without formality (see The Computer Journal, Vol. 19, p. 287, final paragraph).
List of symbols and their representation:
| [] | A blank. Printed like a half box. |
| [10] | The ten for the exponent in a real-type number. Printed as a small lowered ten. |
| [] | The power operator: an uparrow. |
| [] | The times sign: a cross like an x. |
| [÷] | The integer division operator: a - with a dot above and below. |
| [<] | Simple: less than. |
| [] | Simple: less or equal. |
| [=] | Simple: equal. |
| [] | Simple: greater or equal. |
| [>] | Simple: greater than. |
| [] | Simple: not equal. |
| [] | Simple: logical equivalence. |
| [] | Simple: logical implication. |
| [] | Simple: logical or. |
| [] | Simple: logical and. |
| [¬] | Simple: logical not. |
| [] | The Greek letter Gamma (upper case). |
| [] | The Greek letter Theta (upper case). |
| [] | The Greek letter Sigma (upper case). |
| [] | The Greek letter Omega (upper case). |
HTML-edition: N.Landsteiner (n.landsteiner@masswerk.at) 2001-2002
based on a PDF-document edited by Andrew Makhorin (mao@mai2.rcnet.ru), Department for Applied Informatics, Moscow Aviation Institute, Moscow, Russia.
Original publication:
Modified Report on the Algorithmic Language ALGOL 60.
The Computer Journal, Vol. 19, No. 4, Nov. 1976, pp. 364—379.
Other AGOL 60 related documents to be found on this site:
mass:werk - media environments